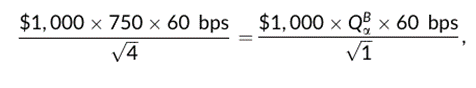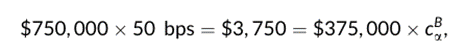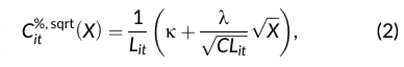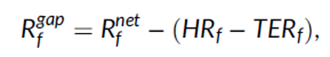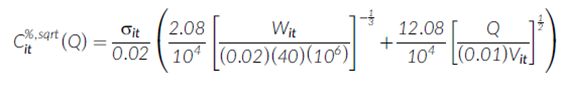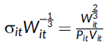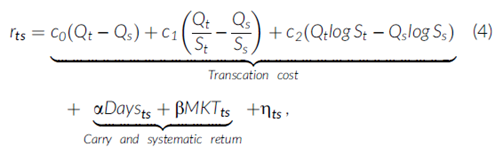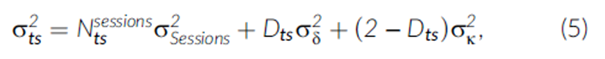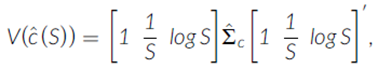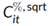专业炒股配资门户 FAJ：拥挤的策略

　　* 此项目由CFA Institute及CFA Society Beijing联合推出。

　　 The Financial Analysts Journal创刊于1945年，是CFA Institute主办的投资管理领域专业期刊。2020年，该刊位于社会科学引文索引(SSCI)二区。本中文推介项目得到了FAJ编辑部的授权。

　　 FAJ:拥挤的策略

　　 Transaction Costs and Capacity of Systematic Corporate Bond Strategies

　　作者：Alexey Ivashchenko和Robert Kosowski

　　综述：何山，CFA，李融，CFA

　　审校：白雪石，CFA

　　原文链接：Financial Analyst Journal，Vol.80，Issue4(点击文末“阅读全文”可查看)

　　推荐语

　　本文由阿姆斯特丹自由大学金融学助理教授Alexey Ivashchenko和帝国理工大学金融学教授Robert Kosowski共同完成。

　　本文主要研究系统性量化策略在公司债市场中是否存在“最适规模“的问题。作者以市场微观结构不变性(MMI)假设为基础，构建了V型的债券交易成本函数，并以此分析了包括反转策略、流动性风险策略、信用风险策略在内的9种主流债券系统性量化交易策略是否存在所谓的交易规模限制。其分析表明，各量化策略均存在某一“最适规模”。超过这一规模，策略的交易成本便会上升。其中，以反转和流动性信号为核心的高换手率策略的最适容量较低，约为100亿美元。以信用风险溢价为主要投资考量的低换手率策略的最适容量较高，可达6000亿美元。

　　当前，量化策略已广泛应用于国内的股票、债券、衍生品市场。不同量化策略在国内市场也存在着各自的“最适规模”。量化策略的最适容量可能因策略类型和市场环境而异。中信证券在2023年的研究[1]指出，量化CTA策略和股票市场中性策略的私募基金在收益率最高时的规模大约为5-20亿元，而以指数增强策略为代表的量化基金收益率最高时的规模普遍在50亿元以上。

　　将各策略的最适容量与其国内市场的实际规模对比，我们发现部分策略已面临“拥挤”风险。有的策略甚至已经经历了“发展——拥挤——出清”的完整周期。以股票市场中性策略为例，私募排排网[2]数据显示该策略私募基金截至2023年年末共有142只。若以中信证券测算的该策略收益率最高时的单只基金规模中位数(12.5亿)测算，则估算该策略的最适市场规模约在1775亿元。而根据中信证券[3]测算，2023年年末，股票市场中性策略私募基金的整体规模已达3100亿元，已经超过了该策略的最适市场规模。随后，在2024年，该策略便迎来了“重创”。根据私募排排网数据[4]，2024年股票市场中性策略产品收益率中位数为5.75%，为2019年以来的最低水平。包括幻方在内的多家头部量化私募公司于2024年10月宣布放弃中性策略[5]。至2024年12月，中性策略[6]的市场规模已下降到了约920亿元。虽然2024年中性策略的低迷可能由市场条件、宏观经济形势、监管政策、投资者行为的多重因素导致，但我们认为较为“拥挤”的策略环境可能在一定程度上放大了策略收益率的波动，使得收益风险比下降。

　　关于策略的“拥挤”风险，国内多家媒体也已有相关报道。以中国基金报[7]在2022年的报道为例，包括鸣石、幻方等头部量化私募都表示随着量化投资的快速膨胀，部分策略已进入相对拥挤的阶段。策略的获利难度出现了上升，策略的同质化已开始带来超额收益衰减的问题。

　　这种量化策略的“拥挤”趋势，可能加剧了机构之间的竞争，放大收益率波动，增加了交易成本，压缩了单一策略的收益空间，可能导致中小量化机构难以生存，影响行业多元化发展，并对市场的价格发现功能和稳定性产生干扰。

　　面对此现象，有关部门已经采取行动强化策略监管降低策略集中度，包括强化量化策略备案，引导策略多元化，对“最适规模”较小的高频策略实施惩罚性交易费用等。同时，以鸣石投资为代表的部分量化基金也开发了监测策略拥挤的新模型，部分抵消了策略拥挤所带来的负面影响。

　　本文的分析结果对国内监管和市场微观主体仍有借鉴意义。下一步，监管机构可提升对量化策略的差异化管理，对高换手率策略设置较为严格的投资总量限制，并在风险可控状态下对低频策略设置较为宽松的总规模上限，以防止某一策略过于拥挤而导致的“共输”局面。同时，国内量化机构也应深入挖掘更精细化的市场信息和数据，开发更具独特性的量化策略，探索多种量化策略的融合应用，通过不同策略之间的相互补充和平衡，提高整体投资组合的适应性和盈利能力，减少因策略单一而导致的“拥挤”问题。

　　[1]中信证券.私募证券产品统计观察(2023年第48期)[EB/OL].(2025-05-28).https://www.doc88.com/p-90029771543649.html.

　　[2]私募排排网.私募数据中心[EB/OL].(2025-05-28).https://dc.simuwang.com/

　　[3]中信证券.量化基金：风格逆转考验策略稳健性[EB/OL].(2025-05-28).https://mp.weixin.qq.com/s/dD5AF4hDEg6i86iHn4-DcA.

　　[4]私募排排网.股票市场中性策略年度十强出炉[EB/OL].(2025-05-29).https://www.simuwang.com/news/275667.html

　　[5]澎湃新闻.又一家私募放弃中性策略，全面转向看多？多家百亿私募表示仍看到长期配置价值[EB/OL].(2025-05-29).https://www.thepaper.cn/newsDetail_forward_29121207

　　[6]中信证券.量化基金跟踪与2025年展望：整装再出发[EB/OL].(2025-05-28).https://news.sohu.com/a/858553890_122014422

　　[7]中国基金报.量化策略已进入拥挤阶段？私募：不同策略情况各异[EB/OL].(2025-05-28).https://www.chnfund.com/article/AR20220313103221026

　　01引言

　　学术界和业界对公司债投资中系统性策略和因子策略的兴趣与日俱增。这在一定程度上归因于公司债回报预测的学术研究。同时，自动化或电子交易系统的普及也使得公司债的交易更为便捷。股票市场系统性因子策略的泛化也为债券交易带来了竞争压力。

　　在业界，MSCI等机构制定了包括多因子和ESG主题的公司债指数；贝莱德、荷宝、东方汇理等大型资产管理公司也推出了公司债ETF产品；资产管理公司也在推广系统性公司债交易策略这一概念。公司债券交易的自动化程度已达到约50%，投资组合交易的百分比占比也已达到两位数，这使得公司债券交易和系统性策略的实施比以往更加便捷。

　　系统性策略或基于某因子的投资策略在公司债市场中的资产规模(AUM)落后于同等策略在股票市场的规模。根据晨星数据，截至2020年底，股票市场中可被归类为系统性交易策略的AUM为1.35万亿美元，而公司债市场仅有1436亿美元。系统性公司债策略的追赶潜力巨大，美国股票市场的规模仅比美国公司债市场的规模(从按美元计金额角度)大几倍。

　　由于现有数据和方法论的局限性，公司债券定价的过往学术研究文有至少有两个重要问题尚未解答：第一，系统性公司债券策略在调整实际交易成本后，是否仍然有利可图？第二，系统性公司债策略的容量限制(或者是最适宜的规模)是什么？本文旨在回答这些问题。鉴于公司债市场的特殊性，这些问题并不简单。为克服研究中的障碍，我们借鉴了Kyle和Obizhaeva(2016)关于市场微观结构不变性(MMI)和交易成本函数(衡量交易规模与交易执行成本间的关系)的相关研究，对系统性策略的净回报做出了新的估计。

　　公司债的交易成本难以估计。公司债的交易通常不频繁、且单笔规模大，通常由交易商和投资者通过非匿名的方式协商完成。尽管如此，已有研究成功应用了多种方法估计债券交易成本，包括有效价差、基于回归和规模调整的方法(Edwards、Harris和Piwowar，2007；Harris，2015；Reichenbacher和Schuster，2022)。

　　然而，上述研究无法直接用于估计交易策略的容量限制，因为这些研究都基于历史的公司债交易数据(TRACE)估计的交易成本，其成本函数通常具有负斜率(即大额交易执行成本更低)。这带来了一个问题：在成本函数向下倾斜的情况下，任何系统性债券策略(具有正的总回报)的容量在理论上是无限的。逻辑上，基金规模越大，投资组合再平衡交易的规模越大，每笔交易的成本就越低。

　　这种“规模折扣”的原因是交易商维护客户关系的动机通常导致大额公司债交易的定价通常更优惠。大额投资者和频繁交易的投资者从债券交易商处获得的价格最优。然而，TRACE数据无法识别投资者身份。将不同规模的投资者产生的交易混为一谈，得到的成本估计会显示出“规模折扣”特征。此外，由于交易商报价“非最优”而未完成的交易并没有纳入统计，进一步导致了估计偏差。

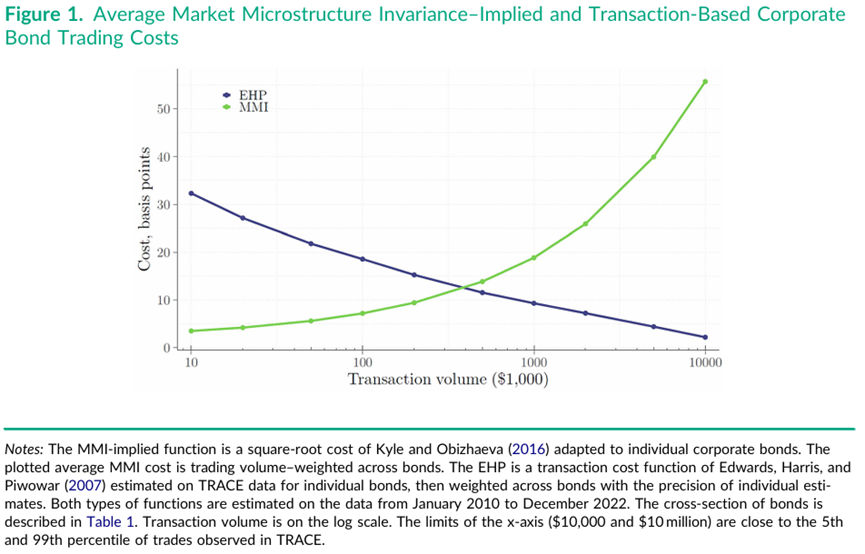
　　基于最新的TRACE数据，我们得出了如下图所示的斜率向下的经典交易成本函数。我们的计算方法基于Edwards，Harris和Piwowar在2007年的研究(以下统称EHP方法)。然而，正如我们提到的，“规模折扣”事实上与实际公司债投资组合产生的交易成本估计相冲突。

　　为解决向下倾斜成本函数带来的缺陷，我们采用Kyle和Obizhaeva(2016)的MMI方法，将其研究的交易成本函数应用至公司债券，从而得到了衡量系统性债券净回报和容量限制的新估计方法。这一成本函数指出，随着交易规模的增加，交易成本将随之上升。我们得出的MMI成本函数与基于TRACE的大额交易成本估计存在显著差异(如上图所示)。

　　为克服交易成本函数负斜率带来的问题，我们采用Kyle和Obizhaeva(2016)提出的市场微观结构不变性(MMI)框架，构建了公司债交易成本函数。成本函数在设计上表示随交易规模增加，交易的成本会上升。我们校准的MMI成本函数与基于TRACE数据估计的大额交易成本函数存在显著差异(见图1)。通过将MMI隐含的价格冲击与基金持仓数据相结合，我们印证了这种向上倾斜的成本函数能更好地解释债券基金"回报缺口"(即报告期内基金净收益与持仓隐含收益的差额)。我们认为MMI估计更准确地反映了大额交易的真实成本——特别是对那些没有议价能力、必须接受交易商报价的流动性接受者(如遵循自动持仓再平衡策略的投资者)而言。

　　认识到MMI与基于交易的成本函数在债券交易成本评估中的各自限制，我们构建了一个复合成本函数：根据交易规模对MMI和EHP函数赋予不同权重。这种复合成本函数呈V形——在200万美元以下的规模交易成本随交易规模的增加而递减，超过该阈值后交易成本随着交易规模的继续上涨而逐渐递增。我们使用这种V形函数来更好地评估系统性公司债券策略的净收益与适宜规模。结果显示，V形函数与MMI成本函数得出的最适容量估计高度一致。

　　为使研究结果与现有文献可比，我们采用现有较有代表性的多重投资组合策略。我们考虑多种双因子组合，分别基于历史风险价值(VaR)、信用评级、过往收益率和流动性指标(Dickerson等和Dick-Nielsen等在2023年相关研究已讨论过在考虑交易成本前这些投资组合的特性)。同时，我们也采用了Chordia等(2017)的研究成果来构建反转组合及其变种(参见Dickerson等在2023年的研究)。这两个组合均基于债券过往收益率的单因子构建，但在对月末交易的处理方式上有差别。与债券定价此前研究不同，我们仅考虑纯多头组合。用共同基金行业的术语来说，债券投资者可将这类规则化纯多头组合视为"风格"或"smart贝塔"组合。我们还纳入了两个广泛市场组合和一个多因子组合。

　　我们基于广泛市场组合策略来估计容量限制。我们通过设置多种筛选和在平衡限制来使我们的理论债券组合更为真实。除此之外，我们通过变更每一个系统性交易策略中每一个基金的投资规模，测算出了在多大规模该策略便不会产生收益。在MMI方法和V型交易成本函数方法下，各种策略的规模“上限”在4.5万亿美元至11万亿美元之间。其中，下限为投资级投资组合，上线为广泛市场组合。平均来看，我们采取样本中的所有债券未偿还额为4万亿美元左右。因此，我们认为公司债投资的市场风险溢价即使在最大的投资组合中仍未被交易成本完全对冲。与晨星此前对系统性交易策略AUM的调查，我们认为系统性公司债投资策略仍有上涨空间。

　　本文与三类文献密切相关：第一类研究债券市场的因子结构与收益可预测性；第二类关注市场微观结构与债券交易成本；第三类研究股票等市场的交易成本调整后表现与容量约束。在这些基础上，本篇文章的创新性在于在估计过程中考虑了各个投资策略的实施限制，并提出了提升系统性公司债交易策略容量限制的方法。

　　02债券样本与系统性债券投资组合

　　数据与样本

　　我们基本遵循既有文献(Dickerson、Mueller和Robotti，2023及更早研究)的样本选择标准，仅纳入"普通型"(非可转换、非资产支持类债券、固定票息、美元计价、剩余期限超过1年等)公司债券。样本时间截至2022年12月的月度数据。债券交易数据来自TRACE(排除名义金额小于1万美元的交易)；债券特征数据源自Mergent固定收益证券数据库(FISD)；发行人特征数据(若为上市公司)来自CRSP和Compustat数据库。

　　本样本与截面债券定价相关研究的经典数据样本存在两点差异：第一，我们仅包含发行规模不低于1亿美元的债券。规模较小的债券通常被排除在主要债券指数之外，交易稀少且缺乏完整的交易价格统计数据。第二，我们对不频繁交易债券的收益采用了差异化处理。

　　学术界的标准做法是：若债券在t月和t-1月的最后五个交易日，或t月的首五个与最后五个交易日存在交易，则确认其t月收益(下文称"末五日"法)。对于交易活跃度低的美国公司债券，这些确认标准过于严苛。我们的“普通型”美国公司债券样本包含约160万个月度债券观测值，其中约21%的债券/月份在TRACE中没有任何交易记录，另有13%的债券/月份在当月首或末五个交易日无交易。"末五日"法将样本缩减至约110万个月度观测值，仅为所有合格未偿债券原始样本的三分之二。

　　虽然"末五日"法适用于横截面定价信号的提取，但系统性策略的收益与交易成本分析需要采用更合理的方法，主要原因有二：第一，债券投资范围理论上应包含所有未偿债券，而组合经理无法完美预测哪些债券未来会有足够交易活动。第二，若组合包含某只当月未交易的票息债券，该债券仍会通过应计利息形式产生"持有收益"(carry)，因此其总预期收益仍为正。

　　基于上述原因，我们采用"估算"的总预期收益来补充"末五日"收益——对于交易稀少或没有交易的债券，其月收益按债券票面利率的十二分之一计算。我们仅在组合绩效评估中使用估算收益，而价格收益构建仍基于"末五日"收益。

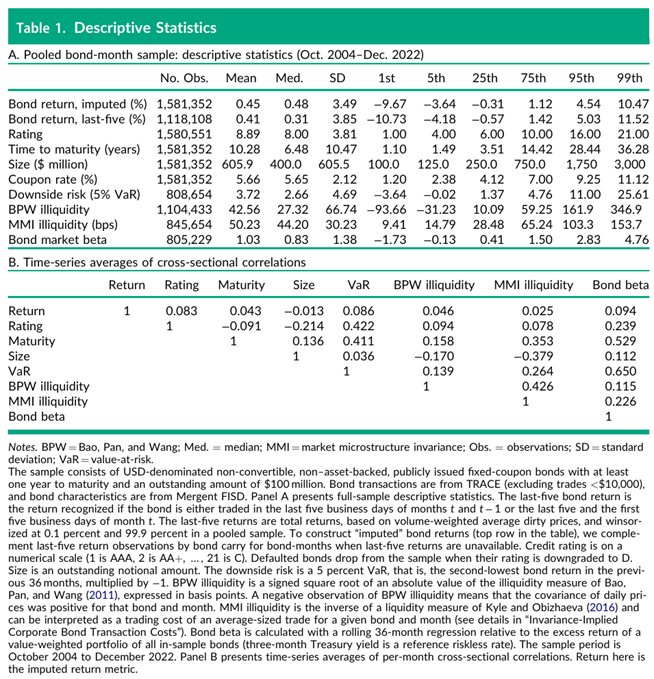
　　表1对比了"末五日"法与我们的债券收益估算方法的差异。两种方法均显示样本债券平均月收益略高于40bps。我们的估算方法在截面上波动更小，且覆盖所有未偿债券。样本中典型债券为BBB评级、票面利率6%、剩余期限约10年、未偿金额近6亿美元。

　　表1的B部分展示了主要投资策略因子的交叉相关性，其中包括信用评级、VaR(三年回溯窗口中月度收益的第二低值)以及Bao、Pan和Wang(2011)构建的流动性指标。这些因子的相关性与Dickerson、Mueller和Robotti(2023)表A2的结果一致。关于MMI流动性指标与隐含债券交易成本的截面数据分析，我们将在"不变性隐含的公司债券交易成本"章节详细讨论。

　　近期vanBinsbergen等人(2024)的研究指出，公司债月度收益中近90%可归因于无风险利率期限结构的变化，这意味着纯信用风险的实际月收益不足10bps。我们在样本中也验证了这一发现。但需要说明的是，本文不探究美国公司债市场中风险被定价的问题，仅评估转移债券交易风险产生的成本——无论这些风险的具体性质如何。

　　基于规则的公司债券投资组合构建

　　在整篇研究中，我们重点构建了以下系统性公司债投资组合策略，这些策略均具有以下核心特征：

　　纯多头配置：所有组合仅持有多头头寸

　　规模加权：除特别说明外均采用市值加权

　　月度再平衡：严格执行每月调仓机制

　　采用共同基金行业的术语体系，债券投资者可将这类规则化投资组合视为：风格策略组合或smart贝塔策略。这九种策略包括：

　　1.全市场组合(MKT)

　　-构成：样本内所有公司债券(包含投资级与高收益债)

　　-加权方式：市值加权

　　2.投资级债券组合(MIG)

　　-筛选标准：所有投资级债券(按ICE美国公司债券指数成分标准)

　　-规模门槛：2017年4月前≥2.5亿美元/之后≥3亿美元

　　-加权方式：市值加权

　　3.信用风险组合(CRD)

　　-排序逻辑：信用评级最低五分位组

　　-交叉控制：在VaR、流动性、历史收益五分位组内等权配置

　　-加权方式：等权配置

　　4.历史风险组合(VAR)

　　-排序变量：三年回溯窗口内第二大月亏损(5%VaR)

　　-筛选标准：VaR最高五分位组

　　-控制变量：跨信用评级五分位等权配置专业炒股配资门户

　　5.流动性风险组合(LIQ)

　　-流动性指标：采用Bao-Pan-Wang(2011)流动性指标衡量

　　-筛选标准：流动性最差五分位组

　　-控制变量：跨信用评级五分位等权配置

　　6.多因子组合(MFP)

　　-组合构成：VAR、LIQ、CRD三等权复合

　　-构建逻辑：纯因子组合持仓重叠度低

　　7.反转策略组合(REV)

　　-信号构建：t-1月收益率最低五分位组

　　-控制变量：跨信用评级组等权配置

　　8.单变量反转组合(R1D)

　　-信号构建：t-1月收益率最低十分位组

　　-研究基础：Chordia等(2017)经典反转策略

　　9.调整版反转组合(REX)

　　-信号优化：剔除排序月末交易日价格波动

　　-方法改进：Dickerson等(2023)调整方案

　　 CRD,VAR,LIQ,REV的各种版本在Dickerson，Mueller和Robotti在2023年的研究中有详细讨论。R1D和REX策略分别基于Chordia等在2017年的研究和Dickerson，Robotti和Rossetti在2023年的研究。后两个投资组合的区别在于是否在估计反转信号时考虑到月份最后一个交易日的价格变动。

　　寻找更好的投资组合并不是本文的目标。我们主要研究交易成本将如何影响纸面债券投资交易规则，因此选择了一些在现有文献中常用的代表性策略。有许多其他系统性债券投资策略在考虑交易成本后具有显著的超额收益(如Israel，Palhares，和Richardson，2018，以及Bertram，Grinblatt，Nozawa，2024)。我们的发现也适用于这些投资组合，因为它们由相似的债券组成，并使用相似的再平衡规则。

　　在构建系统性债券投资组合时，对于“无交易”的月份(即在TRACE数据库中某债券在某月没有任何交易)，我们以最近可用的变量值向前带入。假设某一个债券投资组合每月再平衡一次，仅最多流动性较差的债券。假设某债券在月份t交易，并由于其在t月的流动性得分被纳入t+1月的投资组合。假设该债券在t+1月未交易，将无法计算其在t+1月的流动性得分。我们仍然会根据其在t月的流动性得分将其纳入t+2月的投资组合。

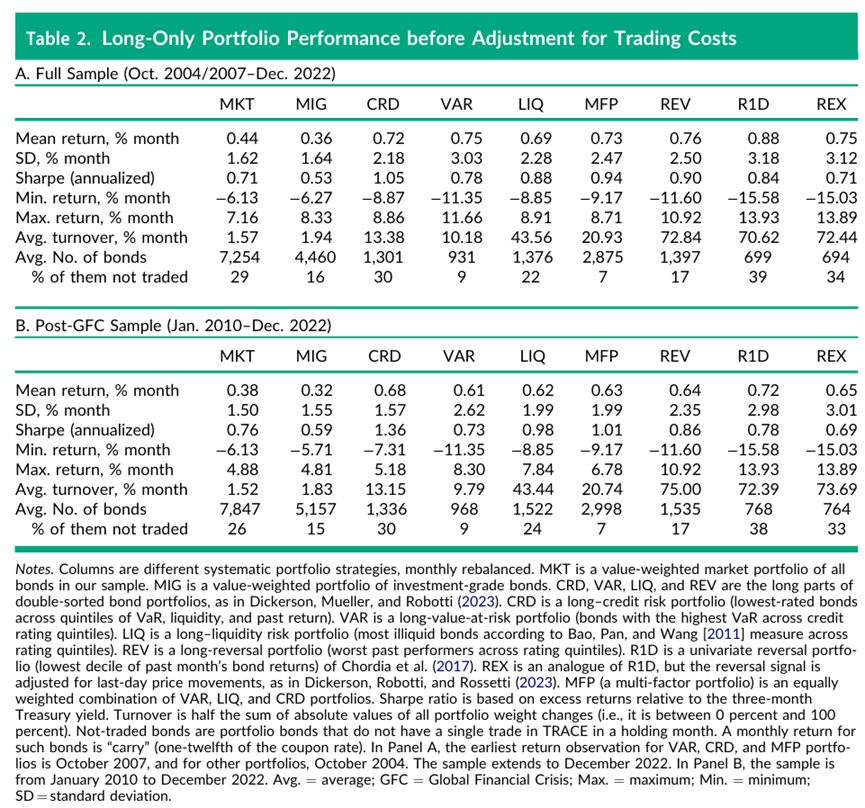
　　表2展示了考虑交易成本前投资组合的特征。表第一部分展示了全样本投资组合的特征，第二部分则聚交于全球金融危机之后时期(2010年1月至2022年12月)。所有考虑的策略在危机后都有相对较高的风险调整后收益，年化夏普比率均超过1。重要的是，这些策略在换手率上的差异很大。反转投资组合的换手率最高，其三种子类型换手率换手率超70%。LIQ的换手率也非常高，危机后时期每月大概43%。VAR和CRD策略的换手率比LIQ投资组合低几倍，这得益于信用评级和历史回撤的变化相对温和。结合VAR，LIQ和CRD策略的多因子投资组合MFP在换手率和债券持仓数量上相对于DeMiguel等人2020年构建的股票多因子投资组合改进有限。平均而言，三因子投资组合的合并持仓每月大约包含3700只债券，MFP也包含3700多只债券，其换手率仅略低于单因子组合换手率的加权平均值。最后，在纸面上，市场投资组合每月持仓换手率约为1.5%至2.0%。

　　表2还凸显了债券策略的一个被此前文献忽略的重要特征。大量在t月份包含在系统性投资组合中的债券在t+1月份是并未被交易，这一部分的持仓比例可以高达40%。我们因此对它们的市场价格了解甚少，更不用说成本了。然而，如果策略的投资规则要求这样做，系统性投资者仍不得不交易这些债券。

　　03市场微观结构不变性(MMI)隐含的公司债券交易成本

　　在本节中，我们将Kyle和Obizhaeva(2016)的交易成本函数应用于单个公司债券，并将其与替代方法进行对比。然后我们将MMI隐含成本与债券共同基金的"回报缺口"(returngap)进行匹配，并提出一种复合债券交易成本函数，该函数融合了MMI和基于交易的估计值。

　　现有文献中并不缺乏对公司债券买卖价差成分的估计(如Bao等2011；Feldhütter2012；Harris2015)。但要估计系统性策略的容量，还需要交易成本中的价格冲击(priceimpact)成分。在这方面，文献遇到了一个障碍：基于交易数据估计的价格冲击呈现向下倾斜的定价函数(Edwards等2007；Reichenbacher和Schuster2022)。大额交易似乎比小额交易执行成本更低。这种效应通常用客户-交易商关系动机来解释(Green等2007；Pinter等2024)。顶级客户(大额且频繁交易者)从交易商处获得最优价格，但TRACE等交易数据汇集了所有层级客户的交易。这是否意味着系统性债券投资者可以随着AUM增长而无限节省价格冲击成本，从而使策略容量实际上无限大？事实并非如此，因为最大交易规模的价格冲击可能仍在上升(我们将在"MMI隐含交易成本与债券基金回报缺口"部分提供间接证据)。我们既无法观察到投资者身份，也无法观察到足够多的高成交量、高即时性交易来识别向上倾斜的定价函数。然而，我们可以利用MMI原理为单个公司债券构建向上倾斜的定价函数。

　　 MMI隐含交易成本估计背后的逻辑

　　本文中，我们将市场微观结构不变性(MMI)作为一种正式工具，用于比较交易指令规模和相关的交易成本。交易规模的特征不能仅用金额来全面描述。在一只通常交易金额仅为100万美元零头的债券中进行100万美元的交易，在其他条件相同的情况下，理论上比在一只经常以该金额进行交易的证券中进行同样100万美元的交易成本更高。同样，对于两只总是以100万美元订单进行交易的证券，其中一只每天交易一次，另一只每天交易10次，那么对于前者而言，新订单是比后者“更大”的事件。下面的例子类似于Kyle和Obizhaeva(2016)的研究，同样适用于公司债券，它有助于读者形成直观理解。

　　假设票面价值为1000美元的证券A每日收益率波动率为60bps，平均而言，该证券每天有四个相互独立的指令(在Kyle和Obizhaeva，2016的研究中称为“投注(bets)”)。考虑一笔750单位证券A的买入单，并假设它处于证券A交易规模分布的第a百分位。如果a=90%，那么遇到大于750单位的订单的概率只有10%。进一步假设执行这笔交易的总成本(包括价格影响)为50bps。基于这些特征，对于另一只同样按票面价值交易、每日收益率波动率相同但平均每天仅交易一次的证券B，我们能对其交易成本该如何衡量呢？市场微观结构不变性(MMI)可以给出答案。

　　市场微观结构不变性(MMI)的第一个假设，即风险转移的不变性，每单位业务时间(以指令到达的频率衡量)内转移的风险金额的分布在各类金融证券中是不变的。这意味着，当基于两个市场运行速度的差异进行调整后，特定债券订单规模分布相同百分位的债券A和债券B的订单，转移的风险金额必定相同：

　　其中，QBa是证券B的第a百分位元指令。风险转移的不变性意味着QBa=375(即遇到大于375单位的债券B订单的概率为1a)。

　　市场微观结构不变性(MMI)的第二个假设，即交易成本的不变性，表明在每单位特定证券的交易时间内，执行转移相同风险金额的订单的成本(以美元计)是相同的：

　　其中，cBa是交易375,000美元证券B的百分位成本。因此，cBa=100bps。

　　因此，两个市场微观结构不变性假设将不同证券的收益率波动率、交易量和交易成本联系了起来。Kyle和Obizhaeva(2016)进一步发展了这一概念，并展示了如何基于不变性原理追踪特定证券的交易成本函数。我们对其进行了调整并将其应用于公司债券领域。在我们的债券交易成本函数中，我们使用TRACE数据来估计特定债券的参数，同时从Kyle和Obizhaeva(2016)对股票市场的估计中借鉴那些不变参数。

　　市场微观结构不变性(MMI)理论并未探讨使不同市场间每单位时间内风险转移的美元成本相等的确切经济机制。从直观上看，如果不同市场中边际投资者的偏好彼此相近，人们就会预期出现类似市场微观结构不变性(MMI)所描述的效果。因此，我们预计市场微观结构不变性(MMI)理论在一体化程度更高的市场中会发挥得更好。市场微观结构不变性(MMI)理论最初是在大型机构股票投资组合的调整操作中得到验证的，这表明存在一类投资者，他们很可能也是公司债券交易中规模最大的参与者之一。

　　市场微观结构不变性(MMI)隐含的交易成本函数

　　我们按如下方式构建市场微观结构不变性(MMI)隐含的债券交易成本。

　　在第t个月交易的债券i。对于每一只这样的债券，我们首先将市场微观结构不变性(MMI)的衡量流动性不足程度的变量1/Lit定义为：

　　其中，Vit是日均(美元)交易量(ADV)，σit是债券的日收益率波动率。C=2000且m2=0.25是由Kyle和Obizhaeva(2016)校准的市场微观结构不变性(MMI)参数，并且这些参数在各个金融市场中被认为是不变的。1/Lit代表在第t个月债券i的一笔平均交易量交易的总成本(包括买卖价差和价格影响)。平均每美元交易量所转移的风险(以收益率波动率衡量)越高，执行一笔交易的总成本就越高。市场微观结构不变性(MMI)理论指出，经过适当调整后，类似风险转移的美元成本在不同市场间应该是不变的。在这样的假设下，为股票交易中的风险转移所估计的某些流动性不足参数也适用于公司债券交易。

　　市场微观结构不变性(MMI)理论并不规定交易成本函数的确切函数形式。相反，它对所选择的交易成本函数的参数施加限制。在本文中，我们考虑平方根形式的交易成本函数。那么，在第t个月交易价值X百万美元的债券i的市场微观结构不变性(MMI)隐含的百分比成本为：

　　其中，j=0.04883且k=0.30721是由Kyle和Obizhaeva(2016)的估计得出的，并且在市场微观结构不变性(MMI)理论下，这些参数在不同资产和时间上必须是不变的。附录A详细阐述了Kyle和Obizhaeva(2016)的研究与交易成本函数(2)之间的关系。

　　公式(2)定义了一个随时间变化且针对特定债券的交易成本函数，其中交易成本的固定部分与流动性不足1/Lit成正比，而价格影响与(1/Lit)3/2成正比。由于随时间变化的流动性不足本身是交易量和波动率的函数，所以市场微观结构不变性(MMI)交易成本函数的参数会随着债券收益率波动率和平均交易量的变化而变化。

　　公司债券交易的稀缺性以及单个债券价格的高度分散性使得对交易成本函数(2)的参数评估变得复杂。当一个月内只有少数几个交易日时，债券日收益率波动率的估计就不太准确。单个债券的交易量在时间上也不具有持续性。这两个因素的比率可能会变得非常不稳定，尤其是在交易量较低的情况下，这意味着一只流动性不足的债券可能会突然变得非常具有流动性，反之亦然，而且这种情况可能过于频繁。

　　为了稳定交易成本的估计，我们通过以下方式计算样本债券的市场微观结构不变性(MMI)流动性不足和交易成本：

　　我们仅为每月至少有五个工作日进行交易的债券计算收益率波动率和日均交易量(进而计算市场微观结构不变性(MMI)的流动性不足程度)。

　　对于每个月t，我们分别截断债券横截面中1/Lit值最高的25%的观测值(这种流动性较差的右尾部分主要是由于交易量极低，而非极端的收益率波动)。

　　如果因此我们在第t个月缺失了债券i的1/Lit数据，但该债券在t月之前的某个月有更早的流动性数据，我们将其直接带入到第t个月(这些延续的数据填补了没有或几乎没有交易的月份以及流动性极端不足读数的月份)。

　　对于每只债券，我们通过取三个月的向后移动平均值来平滑{1/Lit}的时间序列。

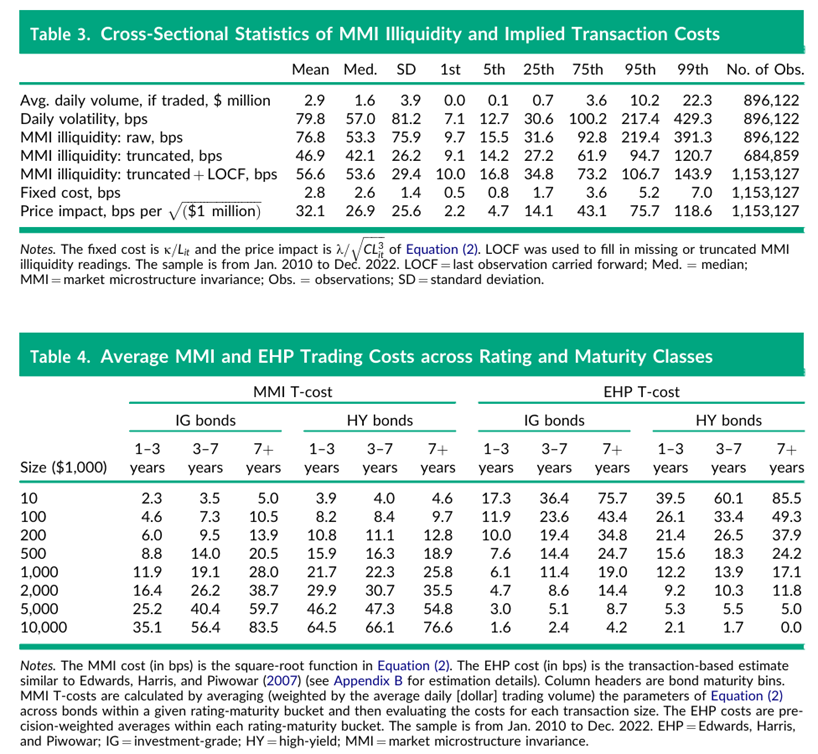
　　按照上述步骤，我们为样本中大多数债券月度数据赋予了交易成本。表3展示了市场微观结构不变性(MMI)隐含交易成本的横截面特征，并突出了上述步骤中的第二步和第三步对这些特征的影响。每月至少交易五天的普通债券，其日均交易量约为300万美元。这样的债券日收益率波动率为80bps(即每日价格收益率的标准差，不包括应计利息)。每月至少交易五天的债券，其平均的全部交易成本约为77bps(中位数为53bps)。

　　每月截断25%最高的流动性较差数据后，市场微观结构不变性(MMI)样本交易成本均值降至47bps。更重要的是，截断操作使得市场微观结构不变性(MMI)衡量流动性的变量分布右尾的流动性不足程度从220到390bps降低至95到120bps。将过去的流动性不足观测值延续到缺失和被截断的债券月度数据中，使得横截面的流动性不足程度均值上升至57bps，右尾数值大约在105到150bps之间。

　　这得出平均固定成本(买卖价差的一半)约为3bps，但每交易100万美元债券产生的价格影响高达32bps。表4展示了市场微观结构不变性(MMI)债券交易成本如何随债券信用质量和剩余到期期限而变化，并将市场微观结构不变性(MMI)成本与基于交易的估计值进行了对比，这与爱德华兹(Edwards)、哈里斯(Harris)和皮沃瓦尔(Piwowar)(2007)的研究类似。在投资级债券中，对于所有交易规模而言，长期限债券的市场微观结构不变性(MMI)交易成本明显高于短期限债券。例如，交易一只剩余期限为10年的公司债券100万美元的市场微观结构不变性(MMI)成本为21bps，而交易一只剩余期限为2年的公司债券同样金额的成本仅为9bps。在高收益债券中，交易成本最高的也是剩余期限最长的债券。

　　对于规模约为50,000美元的交易(接近TRACE数据中的平均交易规模)，市场微观结构不变性(MMI)成本和EHP方法估计的成本相当，但在交易规模较小和较大时，两者存在差异。正如文献中广泛记载的那样，对于小规模交易，EHP成本高于大规模交易的成本。相反，市场微观结构不变性(MMI)成本在小规模交易时低得与事实不符，但由于市场微观结构不变性(MMI)假设中包含的正向价格影响，对于规模为1000万美元的交易，成本会增加到30至80bps。值得注意的是，市场微观结构不变性(MMI)和EHP的估计都表明，交易长期限的高收益债券比交易投资级债券成本更低。

　　表5进一步表明，对于构建市场微观结构不变性(MMI)交易成本函数至关重要的市场微观结构不变性(MMI)流动性不足指标，与其他债券流动性不足衡量指标Bao、Pan和Wang(201)提出的BPW流动性不足指标、实际债券买卖价差、无交易天数的百分比，以及债券发行方的股票买卖价差存在正相关性。值得注意的是，市场微观结构不变性(MMI)流动性不足与实际债券买卖价差的相关性是BPW流动性不足指标与实际债券买卖价差相关性的两倍。同样有趣的是，市场微观结构不变性(MMI)流动性不足与实际买卖价差以及零交易天数百分比都具有相当高的相关性，而正如文献中已记载的那样，零交易天数百分比与实际买卖价差的相关性很弱。

　　这项比较分析的关键结论是，市场微观结构不变性(MMI)流动性不足是一个合理的衡量单个债券流动性的指标。本文的目的不是提出一个更好的流动性不足衡量指标，而是连贯地评估债券交易成本。与其他流动性指标不同，由于不变性理论，市场微观结构不变性(MMI)流动性指标与一个成熟的债券交易成本模型相关联。市场微观结构不变性(MMI)在衡量平均交易成本方面与其他指标一样合理，这是一个额外且令人安心的实证观察结果。

　　市场微观结构不变性(MMI)隐含的交易成本估计值的一个明显缺点是，对于小规模交易，其成本低得与事实不符。我们在“复合交易成本函数”这一部分通过构建一个将市场微观结构不变性(MMI)和EHP交易成本相结合的复合债券交易成本函数来解决这个问题。

　　 MMI隐含的交易成本与债券基金的收益差

　　为了进一步突出MMI交易成本的实用性，我们展示了它有助于解释债券共同基金的交易成本，这些成本通过基金的“收益缺口”来代理(Kacperczyk、Sialm和Zheng，2006)。收益缺口是指报告的基金收益与隐含的基金收益之间的差异。相反，EHP成本并没有提供这种联系。

　　在本节的分析中，我们使用CRSP无幸存者偏差美国共同基金数据库中报告的基金持仓和基金特征。我们关注那些至少将50%的资产投资于TRACE债券的基金，这些债券构成了本文的主要债券样本(表1)。样本期间与本文的主要分析一样，从2010年1月延续至2022年12月。我们根据MMI和EHP成本函数假设，从连续报告期之间基金持仓的实际变化中推导出基金交易成本的估计值。我们的目标是在基金的横截面上比较隐含成本和基金收益缺口。为此，我们计算了样本期间每个基金的成本和收益缺口的时间序列平均值。基金f的收益缺口为：

　　其中，Rfnet是平均报告的基金净收益，HRf是根据观察到的持仓计算的平均持仓毛收益(假设期末再平衡)，TERf是平均报告的费用比率(包含观察到的费用和费用，但不包括交易成本)。Kacperczyk、Sialm和Zheng(2006)认为，收益缺口反映了共同基金的未观察到的行为，这些行为可能与成本(例如，交易成本)和收益(例如，证券借贷的利润)有关。在本节中，重要的是，在其他条件相同的情况下，收益缺口必须随着(未观察到的)基金交易成本的增加而减少：交易成本越高，相对于持仓收益减去显性成本的净收益越低。

　　表6总结了基金的横截面。样本中的中位数基金大约有1.4亿美元的净资产(平均值更大，为12亿美元)，其月换手率接近7%。中位数基金的费用比率约为每年40bps(每月3.3bps)。样本中近四分之一的基金报告的平均净收益为零或负值。中位数基金的隐含MMI和EHP成本相似，约为每年30到35bps(每月2.4和2.9bps)。平均MMI成本明显高于EHP隐含的成本，这在MMI和EHP成本分布的右尾部存在较大的隐含成本估计差异。鉴于表4中报告的最大交易规模的两种成本函数的差异，这种差异是可以预期的。中位数和平均报告的净收益低于持仓收益减去报告的费用：差异分别为每月约-1.7bps和-3.5bps(分别相当于每年约-20和-40bps)。

　　在表7中，我们在债券基金的横截面上，对隐含交易成本(MMI和EHP)以及其他基金控制变量(规模、换手率和投资组合中的信用风险量，以基金持仓的平均信用评级为代理)进行回归分析。我们将所有右侧变量标准化(均值为零，单位方差)，以便于比较它们对收益缺口的影响。模型1显示，MMI成本单独解释了收益缺口横截面变化的约5%。关系的符号如预期所示：MMI成本每增加一个标准差，收益缺口进一步扩大2bps(隐含MMI成本较高的基金净收益较低)。模型2表明，EHP成本未能解释基金收益缺口的横截面变化(关系的符号错误，且解释的方差不到1%)。模型3在多变量回归中确认了这一结果，同时包含MMI和EHP成本，而模型4和5通过控制基金规模、换手率和基金投资组合中的信用风险量，进一步验证了这一发现。MMI成本对基金收益缺口的影响在不同模型规范下保持稳定，约为每月-2bps，每增加一个标准差的成本。在线补充材料中的图A5为表7中的结果提供了图形证据。

　　交易基础的EHP成本呈下降趋势，而上升的MMI成本更适合用收益缺口来代理共同基金成本，这两者之间是否存在矛盾？这两个事实是一致的。每个债券的EHP估计值是从不同投资者的交易汇总而来的。很可能汇总样本中的小交易和大交易并非由同一投资者执行。大投资者获得更好的执行，因此EHP成本估计中出现了“量大从优”的现象。然而，每个投资者在尝试交易较大份额时可能都会观察到正的价格影响。如果是这样的话，那么MMI确实应该更好地拟合代理基金成本的横截面——而它确实做到了。

　　复合交易成本函数

　　上述讨论的每种交易成本评估方法都有其优势和劣势。EHP成本是数据驱动的，可能很好地捕捉了小债券交易的成本，但缺乏大交易规模的递增价格影响。MMI成本通过构造产生递增的价格影响，并有助于解释公司债券共同基金收益缺口的横截面变化，但与小交易规模的数据不一致。为了增强我们净成本债券绩效评估的实用性，我们提出了一个复合交易成本函数，将EHP和MMI方法的优势结合起来。

　　我们提出的复合交易成本函数，也称为本文中的“V形成本”，是MMI和EHP成本函数的加权平均值。对于给定的交易规模X(以百万美元计)，V形成本如下所示：

　　其中γ是待校准的常数。我们在本文的其余部分中将γ设为7。在这种参数设定下，当交易规模为10万美元时，EHP成分在复合成本中的权重为0.98；当交易规模为100万美元时，权重为0.86。在500万美元时，两个成分的权重大致相等，而在1000万美元时，MMI占主导地位，权重为0.75。单个债券的EHP成本估计对个体估计误差较为敏感。按照Edwards、Harris和Piwowar(2007)的原始方法，我们考虑了按到期日、评级和未偿金额相似的债券平均的EHP成本。因此，在公式(3)中，MMI成分是针对特定债券的，而EHP成分是针对到期日-评级-规模(maturity-rating-size)组别的。

　　图2追踪了按到期日、评级和规模分组的成本函数。对于100万美元以下的交易，V形成本与EHP成本几乎没有差异。在所有到期日-评级-规模组别中，这些交易规模存在“量大从优”的现象：交易100万美元比交易10万美元更便宜。对于超过100万美元的交易规模，MMI成分的权重增加，并最终在超过200万美元的交易中产生递增的成本函数。在1000万美元时，交易(单向)短期投资级债券且未偿金额较大的V形成本约为15bps：大约是交易相同金额的长期小型投资级债券成本的六分之一。对于给定的交易规模，按照经济直觉，成本(无论是EHP还是MMI，进而也是V形)随着到期日和信用风险的增加而增加，并随着债券未偿金额的增加而减少。

　　04成本调整后的系统性公司债券回报与容量

　　我们现在转向评估表2中系统性债券策略的成本调整后表现。在此阶段，我们没有施加任何额外的再平衡限制，并假设策略建议的每一个月末再平衡交易都被执行，因此承担了完整的交易成本。如果某债券在再平衡月份错过了MMI流动性读数(如果该债券未交易或其流动性读数被截断且没有该债券的先前流动性读数)，则我们将其分配为该月份所有投资组合债券流动性分数的平均值。

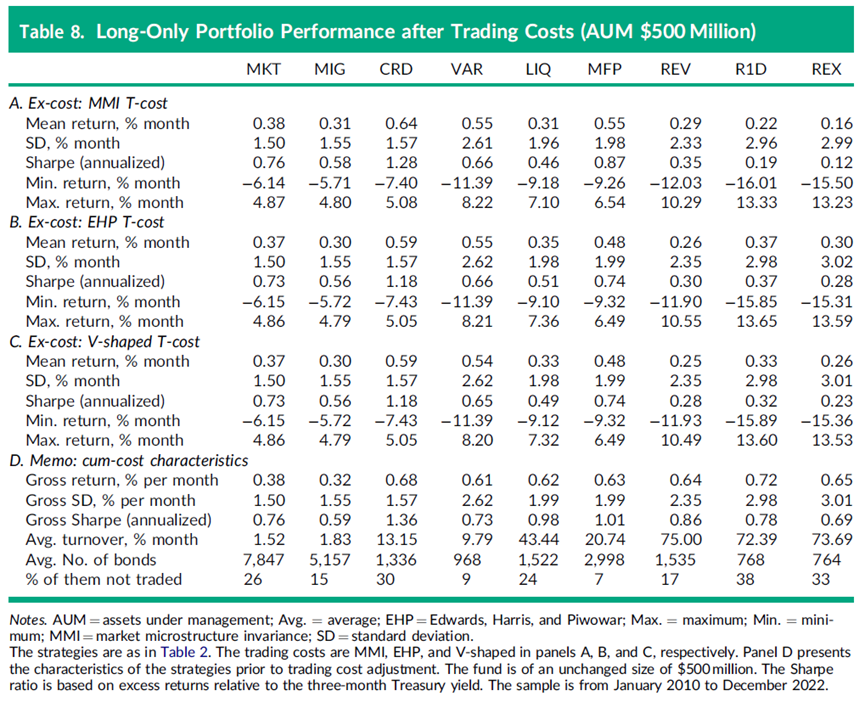
　　表8展示了每月再平衡基金的结果，该基金完全投资于其中一个系统性投资组合，且资产管理规模(AUM)为5亿美元。正如预期的那样，高换手率的反转和流动性策略受到交易成本调整的打击最为严重。它们的夏普比率相对于未考虑成本的情况下降了数倍。LIQ投资组合比其他此类策略表现更好，其成本调整后的夏普比率接近0.5。经过微结构噪声调整的反转策略(REX)在该组中表现最差，夏普比率为0.12(MMI成本)到0.28(EHP成本)。REX的MMI成本明显高于EHP成本，这表明该策略的典型再平衡交易规模大于50万美元(在这个交易规模下，MMI和EHP成本接近)。

　　表8还报告了信用(CRD)和VaR投资组合由于交易成本调整而导致的夏普比率下降幅度较小，与反转投资组合相比。这两种策略都产生了大于0.6的成本调整后夏普比率，其中CRD大于1。然而，这一结果可能需要谨慎对待，原因有二。首先，交易成本估计对于主要由低评级债券构成的CRD投资组合自然是最不可靠的。其次，每个月，CRD投资组合中有很大一部分债券没有TRACE交易记录，这增加了交易CRD策略的固有不确定性。

　　多因子投资组合(MFP)是LIQ、CRD和VAR投资组合的混合体，继承了原始源投资组合的稳健成本调整后表现。DeMiguel等人(2020)展示了多因子股票投资组合如何通过抵消相反符号的交易来节省交易成本。这在MFP债券投资组合中只在有限程度上适用，因为原始投资组合没有太多重叠的持仓。我们发现，与CRD投资组合相比，MFP投资组合的换手率更高，成本调整后的夏普比率更低。

　　对于5亿美元AUM的市场投资组合(MKT和MIG)，由于换手率较低(每月约1.5%到1.8%)，其成本调整后的风险调整表现与风险更高的VAR和MFP投资组合相当。在这种换手率水平下，对于这种基金规模，即使较小的再平衡交易按EHP和V形交易成本模型的不利定价，交易成本对表现的影响也是微不足道的。

　　还值得注意的是，在我们的计算中，那些有大量债券没有TRACE交易记录的策略由于缺失回报的估算而机械地具有较低的回报波动率。回想一下，我们假设未交易债券的月回报是其应计利息，即票息的十二分之一。因此，债券在我们的数据集中没有交易的月份越多，其回报波动率就越低。包含很少交易或未交易债券的债券投资组合的波动率比如果单个债券总是交易时的波动率要低。在线补充材料中的表A1展示了如果我们将“已交易”部分的投资组合的平均回报估算为未交易债券的回报，那么债券策略的成本调整后表现会如何。在这种假设下，CRD投资组合的净夏普比率大约下降了四分之一，至0.9。

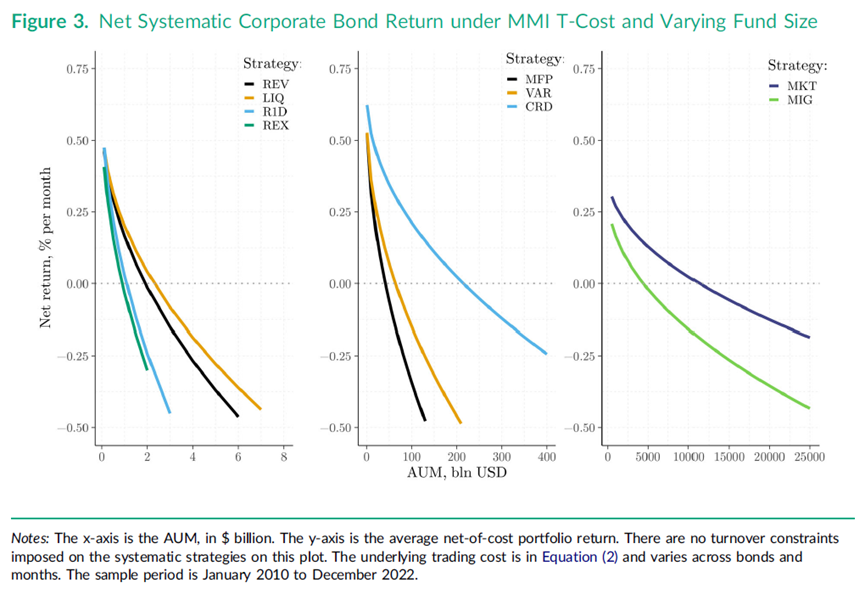
　　图3描绘了在MMI交易成本下系统性公司债券策略的可扩展性。在x轴上，我们变化基金规模，y轴追踪成本调整后的平均月回报。在我们的定义中，净回报降至零的基金规模就是容量限制。图3显示，没有换手率限制的反转策略的容量相对有限，不超过30亿美元。这个数字应该被解释为可以有利可图地投资于该策略的基金的总规模，假设这些基金以相同的方式交易和再平衡。VAR和CRD策略的可扩展性要大得多，容量分别延伸到650亿美元和2150亿美元。市场策略的容量约为4.4万亿美元到11.3万亿美元(MIG和MKT，后者更高)，这比各自投资组合中债券的总名义金额还要大。MMI和V形成本假设下的容量限制差异可以忽略不计，因为只有V形函数中的MMI成分产生了随着交易规模增长的价格影响，从而暗示了策略的容量限制。

　　05实施限制与容量

　　在本节中，我们通过施加实际动机的债券选择和再平衡标准，使理论投资组合更加现实。我们首先描述这些实施限制，然后求解受限制策略的容量限制。

　　实施限制

　　相对缺乏流动性的场外交易(OTC)公司债券市场并不是高换手率系统性交易的最理想场所。由于实施限制，理论债券投资组合很难在实践中复制，这些限制大多与在目标再平衡日期附近交易特定债券的期望数量的可行性有关。因此，债券投资者通常遵循旨在减少投资组合换手率和“过度”交易的规则。在本节中，我们将一些这样的规则整合到我们的系统性债券投资组合中，以更好地了解更具可行性的债券策略的成本调整后回报。我们考虑的规则如下：

　　禁止零售规模交易：如果再平衡交易的规模为零售规模(小于10万美元)，则不执行该交易，该债券的美元头寸保持不变，直到下一个再平衡日期。这是大多数大型公司债券投资者遵循的规则，因为小幅度的投资组合调整(例如，如果是一个基准投资组合，降低跟踪误差)的好处并不能抵消成本(这在原则上不仅包括货币交易成本，还包括基金交易员协商场外交易的努力)。

　　部分再平衡：我们只执行策略建议的最大的三分之一的再平衡买入和卖出交易。部分再平衡旨在通过偏离原始投资计划和稀释预期回报信号的成本来减少投资组合换手率。一位经验丰富的债券交易员告诉我们，在实践中微调部分再平衡规则“更多是艺术而非科学”。我们选择了一个简单的“三分之一”规则，因为它仍然突出了部分再平衡对债券投资组合表现的影响，并且易于实施。每当再平衡交易未能通过部分再平衡门槛时，该债券的美元头寸保持不变，直到下一个再平衡日期。本文中唯一对部分再平衡(以及零售规模交易限制)的例外是，当债券退出投资范围时(例如，因为它的到期时间少于一年，或者由于部分回售导致其未偿金额低于1亿美元)。在这种情况下，无论交易规模如何，都会平仓。

　　抽样：我们只考虑原始系统性投资组合中权重最大的一半债券，用于纳入抽样投资组合(每个再平衡月份分别考虑)。随着投资组合中持有的证券数量增加，分散化的边际收益会减少。这在公司债券投资组合中尤其相关，因为许多发行方有多个未到期的债券，其中一些在规模和到期日上几乎没有差异。抽样的目的是在不稀释回报信号的情况下减少过度的投资组合管理成本。由于本文中的债券投资组合不是等权重的，最大的50%持仓代表了原始投资组合价值的65%到85%。

　　基于过去交易活动的选择：公司债券交易不频繁，债券投资组合经理通常将过去的交易活动视为未来债券流动性的相关预测因子。因此，选择过去交易活动较高的债券而非较低的债券进入投资组合。交易量和交易次数都可以衡量过去的交易活动。据传闻，后者更受债券经理的青睐，因为(a)实时TRACE记录不会报告超过监管上限的交易量，(b)单一过大的交易并不能使债券变得流动。在这里，我们将投资组合限制在过去一个月内至少交易了五个工作日的债券。基金经理可以通过观察实时TRACE报告轻松地实施这种选择标准。

　　再平衡限制的机制如下。对于“禁止零售规模交易”和“部分再平衡”，每个月的目标投资组合是表2中的原始无限制系统性投资组合。在t月，由于换手率限制，基金经理不会完全再平衡到t月的目标投资组合，而是得到一个偏离目标的投资组合。在下一个再平衡月份t+1，将t月的偏离目标投资组合与t+1月的目标进行对比，确定符合条件的再平衡交易，依此类推。我们依次实施“禁止零售规模交易”和“部分再平衡”，即部分再平衡的投资组合首先排除零售规模的再平衡交易。对于“抽样”和“基于过去交易活动的选择”，目标投资组合会发生变化。在前一种情况下，每个月的目标投资组合只包括原始目标投资组合的一半持仓。在后一种情况下，这样的抽样一半投资组合进一步限制为过去交易活跃的债券。然后，将t月的实际投资组合与这些修订后的t月目标进行对比，并实施通过“禁止零售规模交易”和“部分再平衡”筛选的再平衡交易。也就是说，上述列出的每个限制都包含了所有先前的限制。

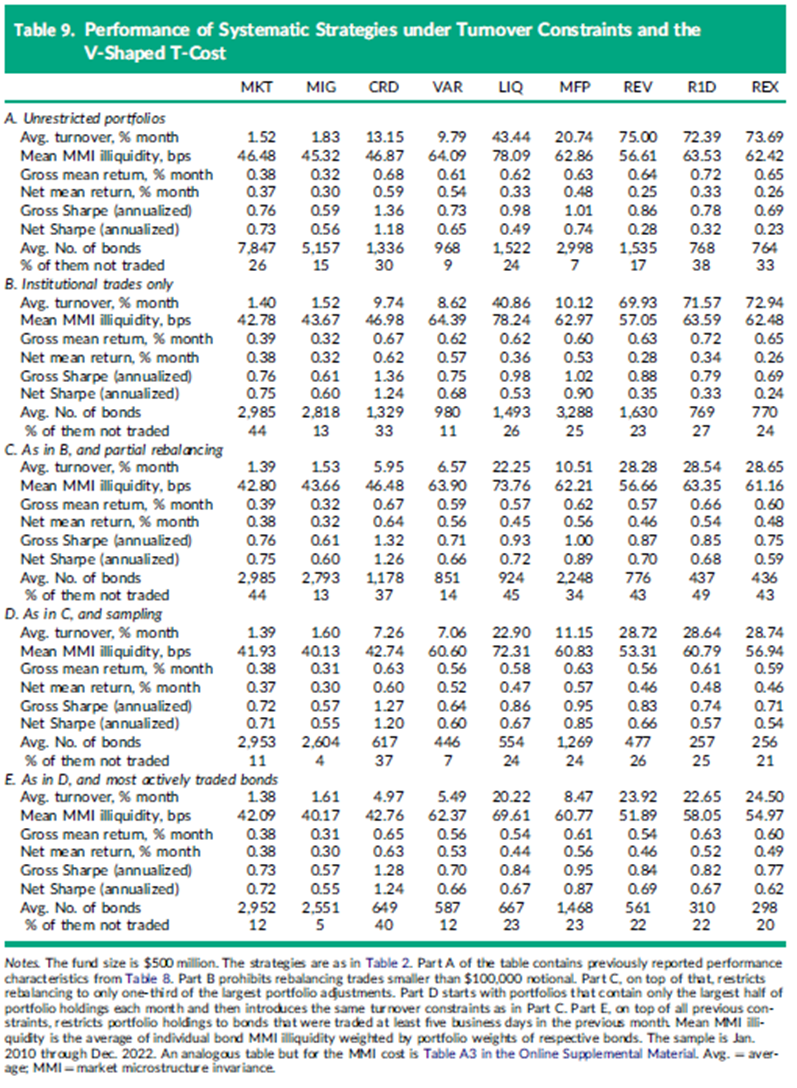
　　表9通过依次向我们的基准5亿美元AUM系统性基金添加实施限制，展示了关键的投资组合表现特征。表9的B部分限制了交易规模为机构规模(无限制的表现见A部分)。禁止零售规模再平衡意味着最小的新持仓不会进入投资组合。因此，受此限制影响最大的投资组合(就持仓而言)是那些最初有许多此类小头寸的投资组合：MKT和MIG。例如，在禁止零售规模再平衡后，广泛市场投资组合(MKT)的平均债券持仓数量从8000个下降到大约3000个。市场投资组合的换手率也有所下降，但由于MKT和MIG投资组合即使只有原始持仓的40%，也已经很好地分散化，因此对表现的影响微乎其微。零售规模交易限制对其他系统性投资组合的影响适中，除了MFP投资组合；其净夏普比率从0.74增长到0.9，换手率下降了一半。具有高无限制换手率和相对较少持仓的投资组合(如R1D和REX)几乎不受零售规模交易限制的影响。这些投资组合在无限制的情况下已经以机构规模进行再平衡。

　　在表9的C部分，我们在零售规模交易限制的基础上增加了部分再平衡限制。这一限制有效地移除了那些足够大以达到机构规模但不足以进入当月最大三分之一再平衡交易的再平衡交易。与无零售规模交易的情况相比，这种限制必然会对高换手率和较少持仓的策略产生强烈影响。事实的确如此：对于所有反转策略和LIQ投资组合，换手率最多下降了三分之二，降至每月20%到30%之间。重要的是，即使在换手率降低的情况下，反转和流动性投资组合的毛表现也没有显著恶化；反转信号只在有限程度上被稀释。在表9的C部分中，所有反转和流动性策略的成本调整后夏普比率相对于B部分都有所提高。对CRD和VAR投资组合的影响适中。对于MFP投资组合，部分再平衡增加了回报波动率(在持仓进一步大幅减少的情况下)，对风险调整表现产生了负面影响。值得注意的是，部分再平衡使整个投资组合倾向于不常交易的债券，这可能并不是一个理想的投资组合特征。最后，部分再平衡对市场投资组合在禁止零售交易限制的基础上几乎没有影响。这是因为对于一个5亿美元AUM的市场投资组合来说，一些最大的再平衡交易是零售规模的，已经在前面的步骤中被过滤掉了。

　　在表9的D部分，我们在抽样投资组合上施加了零售规模交易和部分再平衡的限制，即只包含原始投资组合持仓中最大的一半。与C部分(考虑了完整投资组合)相比，抽样减少了投资组合持仓。此外，它还显著减少了投资组合中未交易债券的比例。然而，在保持基金规模不变的情况下，持仓数量减少意味着更多的机构规模换手率、价格影响和更低的净回报。因此，所有投资组合的成本调整后夏普比率在表9的D部分都比C部分小。将抽样和受限制的投资组合与原始无限制的投资组合(A部分)进行比较，我们发现，对于市场投资组合和VAR策略来说，成本调整后的风险调整表现变差了，但对于所有其他策略(尤其是高换手率的LIQ、REV、R1D和REX)来说，表现有所提高。

　　在表9的E部分，D部分的目标投资组合进一步限制为只包括过去交易活跃的债券。这一额外限制的一个后果是，除了MIG之外，所有考虑的投资组合的换手率都有所下降。这可能是由于单个公司债券的持续交易频率。一个月内交易超过五个工作日的债券集合从一个月到下一个月变化不大。例如，CRD和VAR投资组合的换手率现在约为5%，低于CRSP共同基金数据集中公司债券共同基金报告的平均月换手率(表6)。当降低换手率的好处超过原始信号的稀释时，净回报保持不变或增加(除了LIQ和MFP之外的所有策略)。因此，成本调整后的夏普比率相对于D部分保持不变或增加。鉴于这些结果，我们认为表9的E部分中的投资组合在实际可行性和表现方面优于A到D部分的投资组合。

　　在本节中讨论的受限制投资组合没有明确针对交易成本优化投资组合。G rleanu和Pedersen(2013)考虑了理论上的交易成本优化投资组合，DeMiguel等人(2020)展示了如何在多因子股票投资组合中融入其中一些想法。公司债券交易成本的研究程度不如股票交易成本深入。我们试图推进对可行系统性投资组合表现的个体债券交易成本影响的理解。一旦对个体债券交易成本达成共识，明确针对债券交易成本优化投资组合将是未来研究的方向。

　　根据Li等人(2023)和Meli和Todorova(2023)的研究，投资组合交易最近作为交易量的百分比和有资格进行投资组合交易的公司债券宇宙的百分比都有所增长。投资组合交易指的是债券经销商对一组债券进行投标，作为一次交易的一部分，涉及许多单个债券。该交易以全有或全无的方式执行，并且可以将多个经销商置于竞争之中，以对整个篮子进行定价。在未来的研究中，可以将投资组合交易的影响纳入系统性公司债券策略的交易成本和容量估计中。Li等人(2023)表明，投资组合交易可以根据市场条件增加或减少债券交易成本，这意味着对容量限制的影响可能并不直接，而是依赖于市场状态。

　　容量

　　本节迄今为止只考虑了固定规模为5亿美元的受限制投资组合。我们现在讨论受限制的系统性债券策略的容量限制。由于相对交易成本可能随着交易规模的增加而增加，如公式(2)或对于最大交易规模的公式(3)所示，因此存在容量限制。

　　为了估计容量，我们变化一个假设债券基金的规模，并评估交易成本和回报。对于给定的策略，容量限制是基金规模，在2010年至2022年期间，平均每月净回报降至零。我们在这里只考虑MMI和V形交易成本函数，因为向下倾斜的EHP交易成本会产生无限的容量。我们假设，与之前一样，基金的总规模从一个月到下一个月保持不变，并且基金完全投资于美国公司债券。我们考虑了无限制的投资组合以及带有再平衡限制的投资组合。在我们的容量评估中，我们仍然抽象掉了许多实际的经济方面。例如，我们为单一基金行业进行估算(就好像多个基金的资产被汇总在一起，并且再平衡一次性发生)。我们还忽略了随着基金规模变大而可能发生的投资方法的变化。

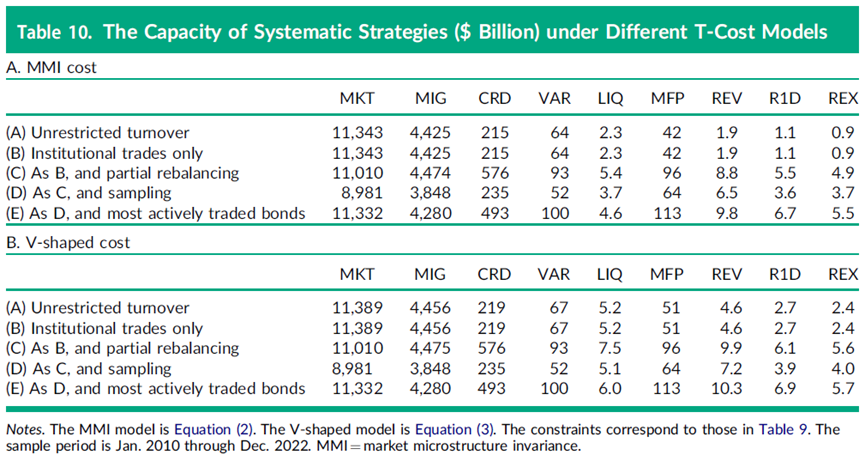
　　表10通过数值求解单一基金AUM，使得相应策略的成本调整后回报为零，从而得到了容量估计。A部分展示了MMI交易成本模型的结果，B部分使用了V形模型。

　　表10的第一行报告了之前在图3中绘制的无限制投资组合的容量限制。反转和流动性策略(LIQ、REV、R1D和REX)由于实施限制而使其容量得到提升。无限制情况下的容量为9亿至52亿美元(具体取决于策略和交易成本模型)，而在最受限情况(E行)下，容量增加至46亿至103亿美元。部分再平衡和基于过去交易活动的限制有助于提升容量。在给定策略和换手率限制下，V形成本模型下的容量更大，这得益于大交易规模下较平缓的价格影响。VAR、CRD和MFP等违约、信用和多因子策略也因实施限制而使其容量提升了两到三倍。对于反转投资组合而言，部分再平衡(C行)是显著提升容量的限制因素。重要的是，抽样(D行)削弱了部分再平衡带来的一些收益。基金经理持有的债券数量越少，在其他条件相同的情况下，达到容量限制的速度就越快。然而，对债券交易活动的限制(E行)弥补了抽样所减少的部分。它将容量提升至纯部分再平衡情况之上，对于VAR和MFP策略尤其如此，但对于CRD策略则不然。这些策略的容量限制范围从VAR的1000亿美元到CRD的近6000亿美元。在这样的容量水平下，MMI和V形成本之间几乎没有差异。在两种模型中，大交易的定价几乎相同，这对容量至关重要。

　　市场投资组合策略的容量对实施限制和交易成本模型的选择相对不敏感。对于MIG和MKT，无限制情况下的容量分别约为4.5万亿美元和11万亿美元，在A到C行中保持稳定。这是因为市场投资组合已经非常广泛地分散化，即使在无限制的情况下，换手率也很低。D行(抽样)再次显示了抽样对容量的不利影响：减少市场投资组合中的持仓数量可能不会损害表现，但随着基金规模的不断扩大，最终会损害容量。与之前一样，对过去交易活动的额外限制(E行)允许恢复因抽样而失去的部分容量。过去交易活跃的债券倾向于保持活跃交易，因此更具MMI流动性，从而限制了价格影响。

　　总体而言，表10中的容量估计表明，系统性公司债券投资仍有相当大的增长空间。即使对于反转策略，如果投资组合倾向于更具流动性的债券，并且优化了换手率，也能承受数十亿美元的AUM。低换手率的策略，针对高回撤或信用风险的债券，可以在高达数千亿美元的投资组合规模下产生正的成本调整后回报。我们的多因子投资组合在交易成本方面节省不多，因为各组成部分的信号相关性较低，暗示的持仓几乎没有重叠。最后，即使在最大的可能市场投资组合中，公司债券市场的风险溢价也不会被交易成本完全抵消。

　　06结论

　　我们运用市场微观结构不变性(MMI)原则来评估公司债券的交易成本，并利用这些实证估计来对系统性公司债券多头投资策略按其容量进行排名。与现有的基于交易的债券交易成本估计不同，市场微观结构不变性所暗示的定价函数随着交易规模的增加而增加价格影响。随着债券基金规模的扩大，交易成本中的价格影响部分会将净回报降至零。利用反转和流动性信号的高换手率策略的容量可达100亿美元。以信用风险溢价为目标的低换手率策略的容量可达6000亿美元。这些容量限制是在对投资组合再平衡施加限制的情况下实现的。一个广泛的市场投资组合的容量比我们样本中的市场规模高出数倍，这表明交易成本并没有完全抵消公司债券的风险溢价。我们的容量估计对系统性公司债券策略的投资者和监管者具有进一步的启示。

　　未来研究有几个有趣的方向。首先，Bali等人(2022)最近对公司债券回报可预测性的机器学习方法取得了令人印象深刻的绩效提升。本文中的MMI估计可以扩展，以回答这种可预测性是否会导致在交易成本调整后产生具有统计学和经济上显著表现的投资组合。其次，我们的交易成本估计可以与Patton和Weller(2020)等替代方法进行比较。第三，将ESG和碳排放考虑因素纳入投资组合是最近一个非常重要的研究领域(Diep、Pomorski和Richardson，2022)。了解此类方法的容量限制对于关注这些市场的投资者和监管者来说具有极大的兴趣。

　　附录

　　附录A：用Kyle和Obizhaeva(2016)的方法提取债券交易成本

　　 Kyle和Obizhaeva(2016)使用非公开的股票投资组合转换数据测试微观结构不变性假设，这些数据允许将投资组合元订单与转换经理实施的单笔交易分开。元订单代理了“赌注(bets)”，这是微观结构不变性理论的核心概念。风险转移的美元金额分布以及与这种风险转移相关的成本分布的不变性是Kyle和Obizhaeva(2016)提出的两个不变性假设。如果不变性假设成立，那么从股票投资组合转换“赌注”中估计的交易成本也必须适用于其他资产类别。在这里，我们展示如何将Kyle和Obizhaeva(2016)第6节中的成本函数重写，使其适用于公司债券。

　　假设交易成本函数具有平方根形式，股票投资组合转换意味着以下成本函数参数化，符合市场微观结构不变性(MMI)：

　　 Vit是日均(美元)交易量(ADV)，σit是债券的日收益率波动率

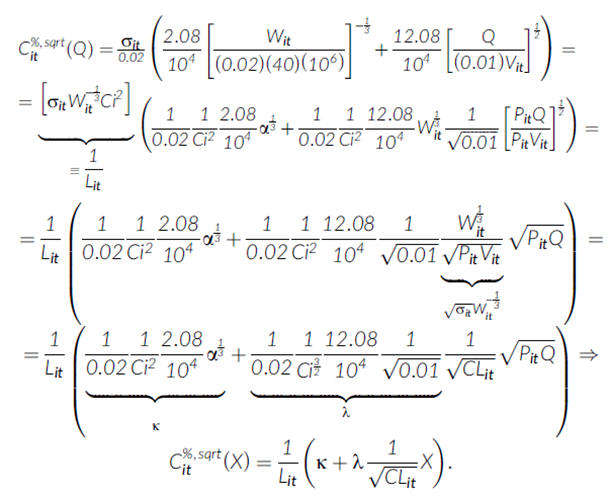
　　其中，σit和Vit分别是股票i在第t天的每日波动率和交易量(以股数计)，Wit=σitPitVit是每日风险转移的美元金额，Q是交易规模(同样以股数计)。该成本函数已针对Kyle和Obizhaeva(2016)样本中的典型股票进行了缩放。这种股票的每日波动率为2%，价格为40美元，平均每日交易量(ADV)为100万股。我们称这种股票的每日风险转移美元金额为α=0.02*40*106。在这种股票中执行相当于其ADV的1%的交易成本为14.16bps，其中2.08bps是买卖价差的一半，12.08bps是价格影响。

　　为了将MMI成本函数应用于公司债券，必须适当地重新调整其比例。以下是我们的方法：

　　其中，C和i2是Kyle和Obizhaeva(2016)中估计的不变参数，X≡PQ是交易的美元金额。i2=0.009886是缩放后的“赌注”大小的对数正态分布的均值，C=2000美元是执行平均规模“赌注”的成本。在上述推导中，我们使用了

　　以及每日风险转移美元金额Wit=σitPitVit的定义，得出

　　通过直接计算，得出κ≈0.04883和λ≈0.30721。我们在样本中的所有个券中保持这些参数不变，正如MMI在不变性假设下所建议的那样。请注意，显性和隐性成本仍将因MMI流动性不足1/Lit的变化而因债券而异。

　　附录B：EHP交易成本

　　我们对EHP交易成本的估计与Edwards，Harris和Piwowar(2007)的方法只有微小的变化。我们使用迭代加权最小二乘法估计以下模型，针对个券公司债券(与本文其余部分一样，在全球金融危机后的样本中)：

　　其中，rts是在连续两次交易日s(较早的交易)和t(较晚的交易)之间的总债券回报。Qt是交易方向(如果客户从经销商处购买则为1，如果客户向经销商出售则为-1，如果是经销商之间的交易则为0)，St是交易的美元金额，Dayts是s和t之间的日历天数，MKTts是s和t之间的市场组合总回报。最后两个因素代表债券特定的持有收益和系统性回报成分。ηts是均值为零的误差项，其方差σts2等于：

　　其中，Ntssessions是s和t之间的交易天数，σsessions2是债券估值的零均值特异成分的方差，σδ2是经销商之间交易的零均值价格让步的方差，σκ2是单个债券交易成本的零均值特异变化的方差。方程(5)中的方差在汇总债券样本中使用与Edwards,Harris和Piwowar(2007)相同的迭代约束最小二乘过程进行估计。给定估计的方差，使用加权最小二乘法重新估计个体债券的模型(4)，权重为σts2的倒数。

　　我们对个体债券的交易成本函数进行正则化：

　　在信用评级-到期-规模组别中。我们考虑两个信用评级组别(投资级和高收益)、三个到期组别(分界点为3年和7年到期)和三个规模组别(分界点为4.5亿美元和9亿美元未偿金额)，总共得到18个信用评级-到期-规模组别。在每个桶中，我们通过将个体债券交易成本函数与估计误差方差的倒数加权，评估横截面平均交易成本函数：

　　对于后续分析，我们将相同估计的EHP交易成本函数分配给同一信用评级-到期-规模桶中的所有债券。如果给定交易规模的成本为负，则用零替换。

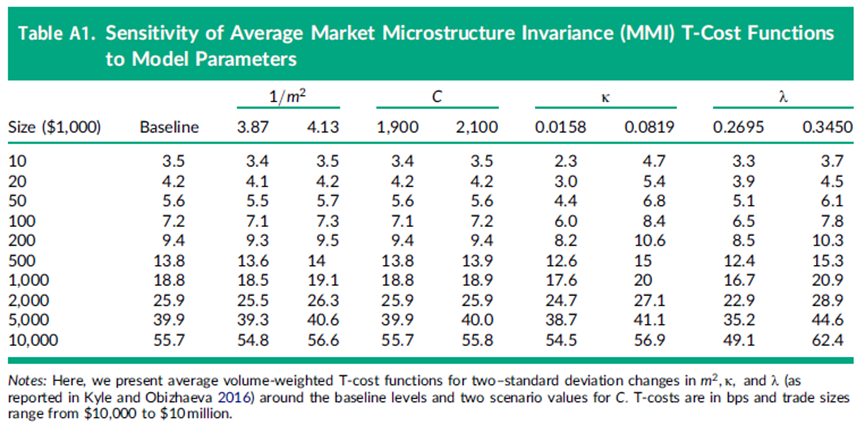
　　附录C：交易成本和策略容量对模型参数的敏感性

　　在本节中，我们讨论市场微观结构不变性(MMI)交易成本以及由此得出的系统公司策略容量如何随模型参数变化。方程(1)和(2)表明，相对于交易规模X的MMI暗示交易成本

　　取决于几个模型参数。这些参数包括：

　　 m2和C(在Kyle和Obizhaeva2016中估计/校准)，它们确定了不变“赌注”规模和成本分布的平均值；

　　κ和λ(同样在Kyle和Obizhaeva2016中估计)，它们将MMI流动性不足1/Lit映射到股票投资组合转换数据中的买卖价差和市场冲击交易成本成分；

　　债券月特定的回报波动率σit和平均每日交易量

　　我们使用TRACE数据进行评估。

　　我们对这些从Kyle和Obizhaeva(2016)“借用”来的参数m2、C、κ、λ的估计误差最感兴趣。这些参数的估计误差可能会影响整个债券面板的交易成本。我们通过以下方式确定本次敏感性测试中参数变化的程度。

　　 C(执行平均“赌注”的全部成本)在Kyle和Obizhaeva(2016)中校准，因此该论文中没有报告C=2000的可靠变化程度。我们选择C的校准值周围的5%区间，即从1900到2100。

　　 m2=C2i6，其中i2是缩放后的“赌注”大小的对数正态分布的均值(见附录A)。均值是使用超过40万个“赌注”观测值相对精确地估计的。i2的平均值周围的两个标准差(均值)约为围绕基线值1/m2=4的3.3%区间。因此，在本次敏感性分析中，我们为1/m2的上下限分别设定为3.87和4.13。

　　κ=(1/0.02)*(1/Ci2)*(2.08/104)*(40*106*0.02)^(1/3)，其中2.08bps是Kyle和Obizhaeva(2016)在表5中为平方根交易成本函数估计的平均市场冲击成本。该估计系数周围的两个标准差得出了κ的区间，从0.0158到0.0819。

　　κ=(1/0.02)*(1/Ci3/2)*(12.08/104)*(0.01)^(1/2)，其中12.08bps是Kyle和Obizhaeva(2016)在表5中为平方根交易成本函数估计的平均买卖价差成本。该估计系数周围的两个标准差得出了λ的区间，从0.2695到0.3450。

　　表A1显示，平均债券交易成本对“赌注”规模的估计误差相对不敏感。比平均“赌注”规模高两个标准差意味着1000万美元交易的成本(56.6bps)仅比基线水平(55.7bps)高出不到1bp。同样，比平均值高5%的C值只会使大交易的平均成本变化几分之一个基点。正如预期的那样，成本对买卖价差和市场冲击参数(分别为κ和λ)更为敏感。λ增加两个标准差会使1000万美元交易的成本增加约6bps。这与较不激进地截断MMI流动性不足分布(在线补充材料中的图A3)的效果相当。

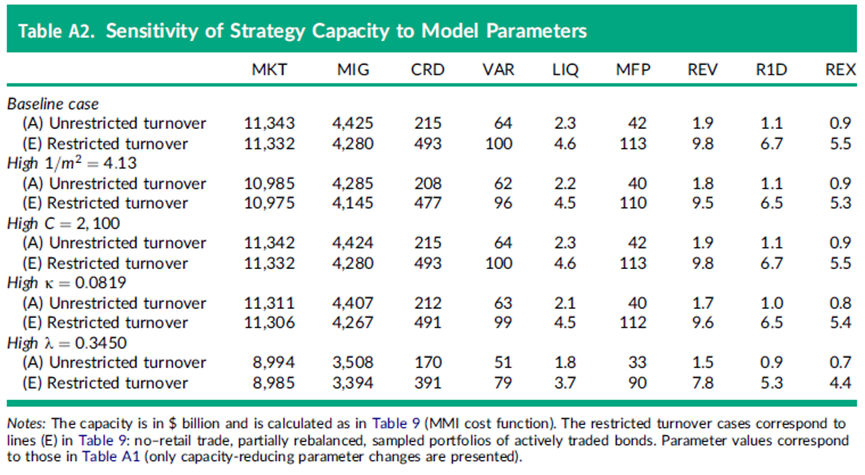
　　表A2展示了我们的容量估计对参数m2、C、κ、λ的敏感性：仅关注降低容量的参数变化，我们发现即使是市场冲击参数λ增加两个标准差，容量也仅适度降低20%。例如，CRD策略的容量从大约5000亿美元降至4000亿美元。在这种更高的λ值下，整个市场投资组合(MKT)的容量约为9万亿美元，这仍高于我们样本中债券的总未偿金额。容量估计对其他模型参数的合理变化甚至不那么敏感。

　　结束专业炒股配资门户

优速配资提示：文章来自网络，不代表本站观点。